テブナンの定理は、複雑な電気回路を簡略化して解析するための重要な定理である。以下にその主要な特徴をまとめる。
定義
テブナンの定理とは、複数の電源を含む複雑な回路を、単一の電圧源と内部抵抗からなる等価回路に置き換えることができるという定理である。
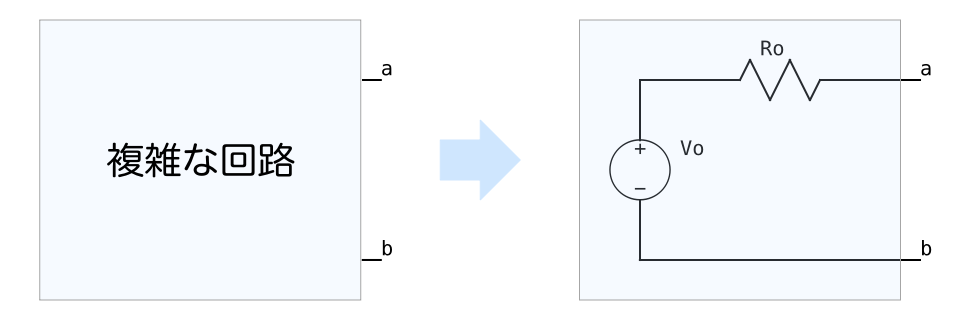
例えば
例えば、下記左側の回路を右側の回路のように等価回路化ができる。
等価回路化の手順
等価回路化の手順は以下の通りである。
① Vo : 元の回路においてa端子とb端子に何も接続しないときのa端子とb端子の間の電圧を求め、これをVoとする。
② Ro : 元の回路において電圧源を0Vとしたときのa端子とb端子の間の合成抵抗を求め、これをRoとする。
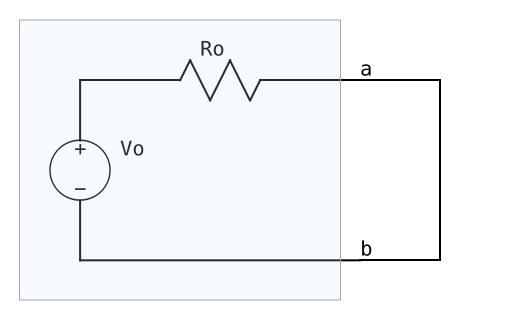
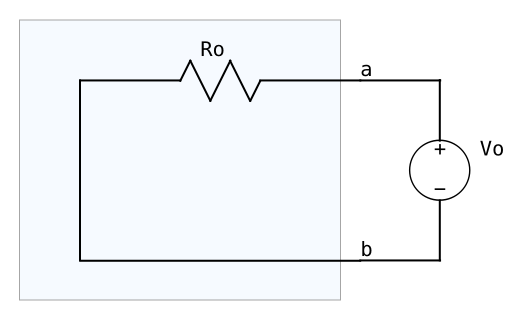
①は直感的に理解できると思うが、②は直感的に理解しづらいので少しだけ補足する。下図の左の回路は等価回路のa端子とb端子を外側でショートしている。この回路ではa端子から外側に向かって I = Vo/Ro の電流が流れる。ここで右の回路のように内側の回路のVoをショートして外側にVoを接続すると、a端子から左に向かって I = Vo/Ro の電流が流れる。このことから②が成立すると直感的に理解できるのではないだろうか。厳密な説明になっていないかもしれないが、シンプルかつ短い説明が直感的に理解しやすいと考えるのでこの程度に留める。
例1
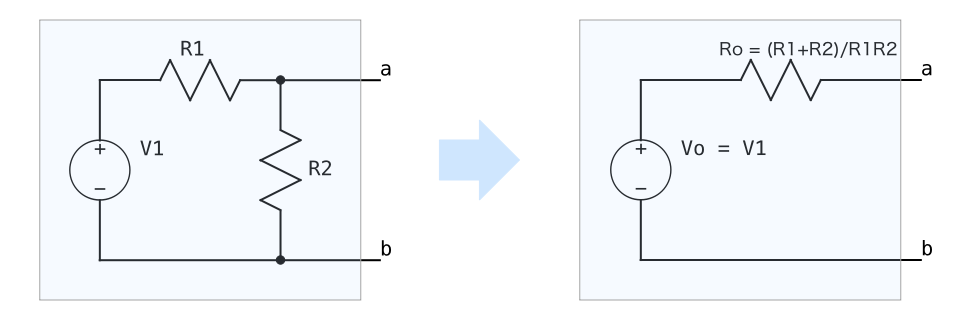
冒頭に述べた例について、改めてテブナンの定理を使って等価回路化する手順を示す。まず、冒頭の例の回路は以下のような回路であった。これを手順①②を用いて等価回路化していく。
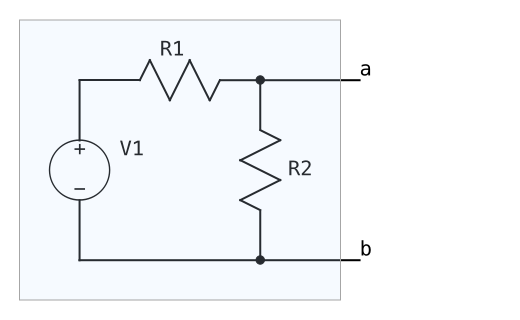
① Vo : 元の回路においてa端子とb端子に何も接続しないときのa端子とb端子の間の電圧を求め、これをVoとする。よって、Vo = V1となる。
② Ro : 元の回路において電圧源を0Vとしたときのa端子とb端子の間の合成抵抗を求め、これをRoとする。よって、Ro = (R1+R2)/R1R2 となる。
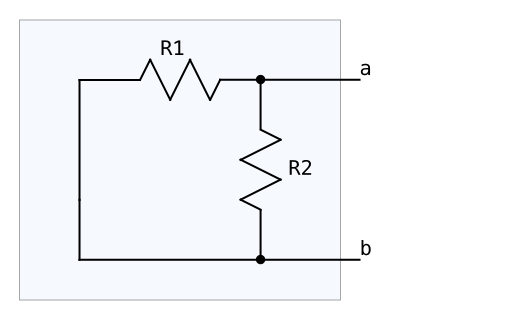
以上より、以下のように等価回路化できる。

例2
別の例として、電圧源が2つある例を示す。
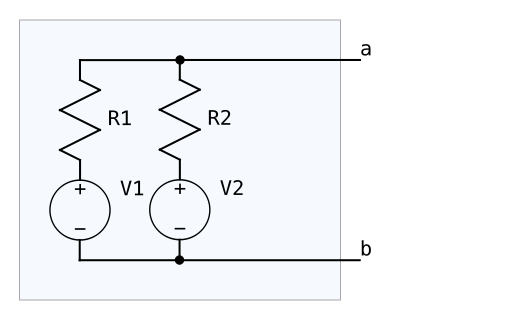
① Vo : 元の回路においてa端子とb端子に何も接続しないときのa端子とb端子の間の電圧を求め、これをVoとする。よって、Vo = (V2 – V1)R2/(R1+R2) + V2 となる。
② Ro : 元の回路において電圧源を0Vとしたときのa端子とb端子の間の合成抵抗を求め、これをRoとする。よって、Ro = R1//R2 となる。
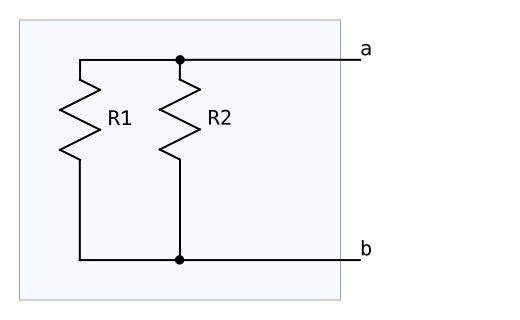
テブナンの定理の別称
テブナンの定理は以下の別称がある。
- 鳳-テブナンの定理
- ヘルムホルツ-テブナンの定理
- 等価電圧源の定理
テブナンの定理のメリット
複雑な回路を単純化でき、回路解析を容易にする。テブナンの定理は、電気回路の解析や設計において非常に有用なツールであり、複雑な回路の振る舞いを理解するのに役立つ。
AC回路への適用
テブナンの定理はAC(交流)回路の解析にも適用可能である。この場合、等価回路の要素はインピーダンスとして扱われ、電圧、電流、インピーダンスは複素数として表現される。周波数依存性を考慮することで、AC回路の解析や周波数応答の計算に広く利用できる。
テブナンの定理の問題点
テブナンの定理は、電気回路の解析において非常に有用な手法だが、その名称の覚えにくさが学習者にとって障壁となることがある。名前を記憶できないことは、往々にして定理の内容自体も記憶に定着しにくいという問題につながる。そして、記憶に定着していない知識は、実際に必要な場面で適切に活用することが難しい。
この課題を解決するため、本記事では以下のような語呂合わせを提案したい。
「手ぶらで 何でも シンプル化」
この語呂合わせには、テブナンの定理の本質が巧みに凝縮されている。「手ぶら」はテブナンの「テブ」を、「何」は「ナン」をそれぞれ想起させる。そして「シンプル化」という言葉は、この定理が複雑な回路を単純化する手法であることを端的に表現している。
この覚えやすいフレーズを活用することで、テブナンの定理の名称と機能を効果的に記憶し、必要な時に即座に思い出すことができるだろう。これにより、電気回路の学習や実務において、この重要な定理をより積極的に活用することが可能となる。
まとめ
テブナンの定理は、どんなに複雑な電気回路であっても、「手ぶらで 何でも シンプル化」 できる定理である。
コメント