ノートンの定理は、複雑な電気回路を簡略化して解析するための重要な定理である。以下にその主要な特徴をまとめる。
ノートンの定理
ノートンの定理とは、複数の電源を含む複雑な回路を、単一の電流源と内部抵抗からなる等価回路に置き換えることができるという定理である。
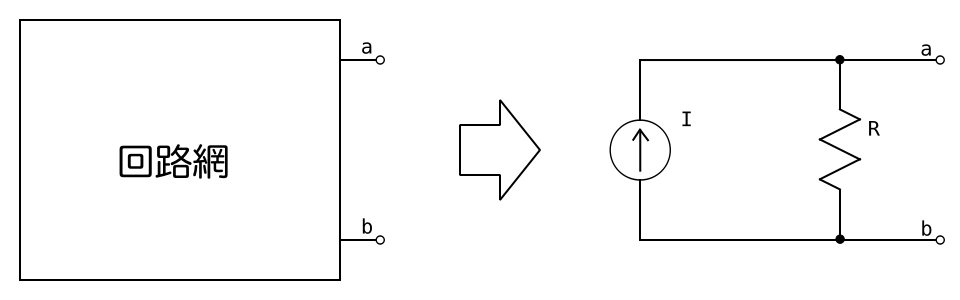
ノートンの定理はわかりにくいため、直感的に理解した方が早い。そのためには、まずテブナンの定理を理解しておくと良い。
テブナンの定理
テブナンの定理とは、複数の電源を含む複雑な回路を、単一の電圧源と内部抵抗からなる等価回路に置き換えることができるという定理である。
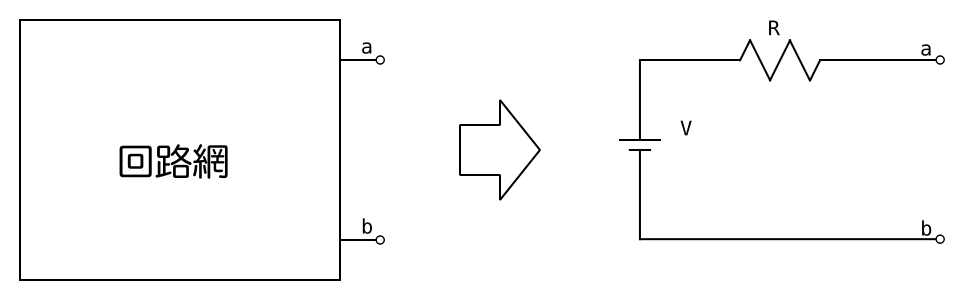
詳しくはこちらの記事を参照
テブナンの定理とノートの定理の関係
テブナンの定理のRとノートンの定理のRは同じである。★重要
このことは、以下のように考えると直感的に理解しやすい。
上図 : ある回路網をテブナンの定理で等価回路化し、ab端子の外側 (右側) に負荷抵抗Rlを接続する。Rl = 0Ωのとき i = V/R (①)となる。Rl = ∞ のとき Vo = V (②) となると考えても良い。
下図 : 同じ回路網をノートンの定理で等価回路化し、ab端子の外側 (右側) に負荷抵抗Rlを接続する。Rl = 0Ωのとき i = I (①)となる。Rl = ∞ のとき Vo = IR (②) となると考えても良い。
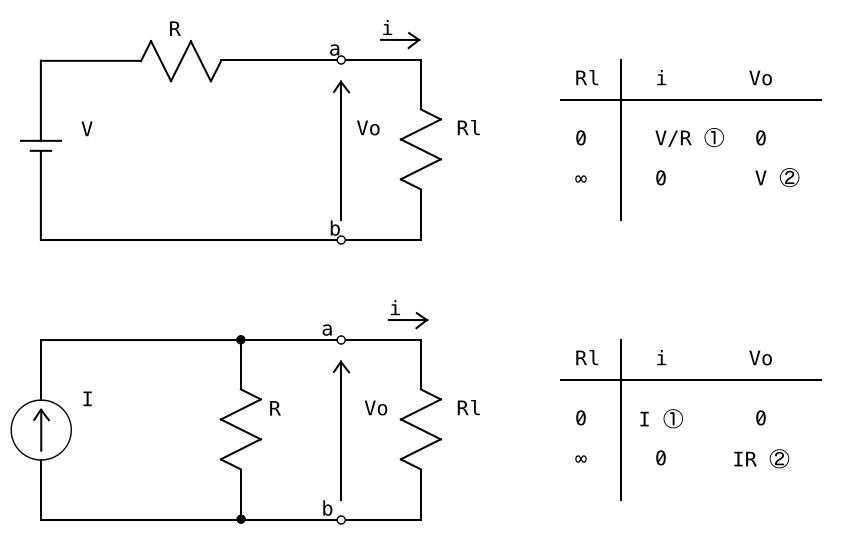
両者の①より i = V/R = I となることがわかる。もしくは、両者の②より Vo = V = IR となることがわかる。いずれかのことより、テブナンの定理のRとノートンの定理のRは同じであると直感的に理解できる。
使用例
AC電流源とパスコンで組まれた回路ブロックがあり、その外部に負荷 (RとC) が接続されている。AC電流をこの負荷に漏らさないようにフィルターのRを入れるとする。 このRの値をいくつにすれば良いか?
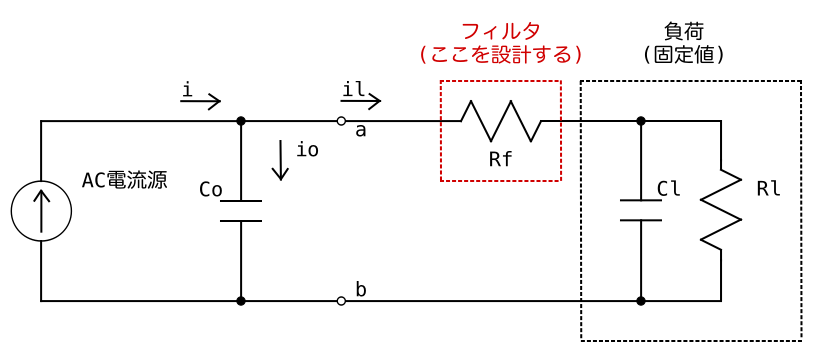
この回路のab端子より左側は偶然にもノートンの定理の等価回路と同じ回路になっている。今回の問題はテブナンの定理の等価回路で考えたほうが簡単なのでテブナンの定理の等価回路に変換したい。まずは、RやCをインピーダンスとして表す。
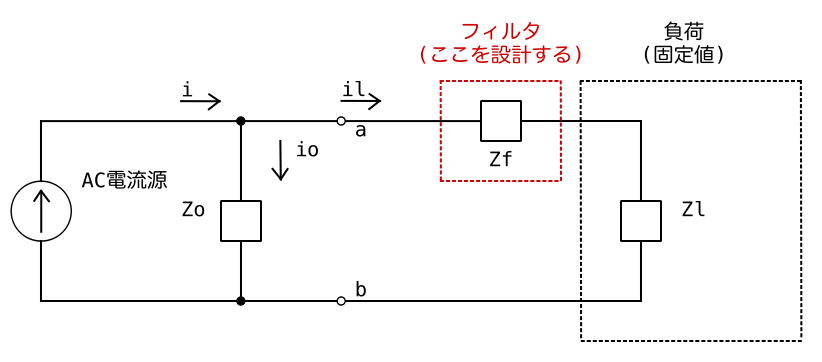
これをテブナンの定理の等価回路に置き換える。
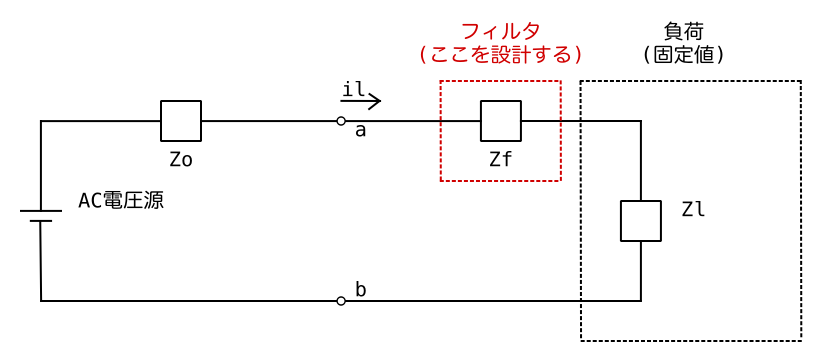
あとは、この回路でZfが無い場合 (Zf = 0) の場合のilを求める。そしたら、それに対してZfをいくつにすればilがいくつに低減できるかが簡単に計算できる。
ノートンの定理の問題点
ノートンの定理は、電気回路の解析において非常に有用な手法だが、その名称の覚えにくさが学習者にとって障壁となることがある。名前を記憶できないことは、往々にして定理の内容自体も記憶に定着しにくいという問題につながる。そして、記憶に定着していない知識は、実際に必要な場面で適切に活用することが難しい。
この課題を解決するため、本記事では以下のような語呂合わせを提案したい。
「ノートン つけ麺 僕イケメン!」
この語呂合わせには、ノートンの定理の本質が巧みに凝縮されている。「つけ麺」の麺1本1本に汁が流れる様は、並列抵抗に電流が流れ分かれる様子を想起させ、複雑な回路の一部がシンプルに見える効果を示している。そして、筆者の個人的な感想としてノートンさんは大変イケメンであり、多分「僕イケメン!」と言ったことがあると信じている。このキャッチフレーズは、ノートンの定理を思い出す際の笑いと記憶に残るツールとして機能する。
この覚えやすいフレーズを活用することで、ノートンの定理の名称と機能を効果的に記憶し、必要な時に即座に思い出すことができるだろう。これにより、電気回路の学習や実務において、この重要な定理をより積極的に活用することが可能となる。
まとめ
複雑な電気回路に出会ったときには、まず慌てずに「ノートン つけ麺 僕イケメン!」と唱えると良いだろう。
コメント