ADCでリセットのデータとサンプルのデータを取って差分する方法は、一般的なADC技術の一つである。この方法は特に以下のような利点がある:
CDS(Correlated Double Sampling)
この技術は、リセットレベルとサンプルレベルの2つの測定値の差を取ることで、オフセットやノイズを低減する。
動作原理:
- リセットレベルの測定: 信号入力前の基準レベルを測定する
- サンプルレベルの測定: 実際の信号レベルを測定する
- 差分計算: サンプルレベルからリセットレベルを引く
利点:
- 固定パターンノイズの除去
- 1/fノイズの低減
- オフセット誤差の補正
応用例
イメージセンサ用の高速ADCでは、CDSが広く使用されている。この技術により、画像の品質が大幅に向上し、低照度条件下でのパフォーマンスが改善される。
実装上の考慮事項
- サンプリング速度: リセットとサンプルの両方を高速に取得する必要がある
- タイミング制御: リセットとサンプルの測定タイミングを正確に制御する必要がある
- デジタル処理: 差分計算を高速かつ正確に行うデジタル回路が必要である
このような差分技術を用いることで、ADCの精度と性能を大幅に向上させることができる。特に、低レベル信号の測定や高精度が要求されるアプリケーションで効果的である。
くし型フィルター
CDS(Correlated Double Sampling)は、信号からノイズやオフセットを除去する手法であり、周波数領域において「くし型フィルター」の特性を持つ。これは、特定の周波数成分を周期的に抑制するフィルターである。
1. なぜくし型フィルターになるのか
CDSは、2つの時刻でサンプリングを行い、その差分を取る。この操作は、2つの時刻でサンプリングした値が特定の周波数では同相となり振幅が2倍になり、特定の周波数では逆相となり振幅が0になるため、周波数応答はくし形(特定の周波数で振幅がゼロになる周期的な構造)になる。
2. 式の導出
時間領域でのCDSの動作を式で表すと、次のようになる。
$$y(t)=x(t)−x(t−Td)$$
ここで、x(t) は入力信号、y(t) は出力信号、Td はサンプリング間隔である。この式は信号の差分を取っているため、CDSの基本的な動作を表している。
この操作を周波数領域に変換するためにフーリエ変換を適用する。入力信号のフーリエ変換を X(f) とすると、出力信号のフーリエ変換 Y(f) は次のようになる。
$$Y(f) = X(f) – X(f) e^{-j 2\pi f T_d}$$
周波数応答 H(f) は出力信号 Y(f) を入力信号 X(f) で割ったものであるため、次のように表される。
$$H(f)=\frac{Y(f)}{X(f)}=1−e^{−j2πfT_d}$$
フィルターの振幅応答は、上記の式の絶対値を取ることで求められる。
$$|H(f)| = |1 – e^{-j 2\pi f T_d}|$$
オイラーの公式を適用すると、次のように展開できる。
$$|H(f)| = |1 – (\cos(2\pi fT_d) – j\sin(2\pi fT_d))|$$
複素数の絶対値の公式を適用:
$$|H(f)| = \sqrt{(1 – \cos(2\pi f T_d))^2 + (\sin(2\pi f T_d))^2}$$
この式をさらに簡単にすると、以下の結果が得られる。
$$|H(f)| = \sqrt{2 – 2\cos(2\pi fT_d)}$$
三角関数の半角公式を適用する。
$$|H(f)| = \sqrt{4\sin^2(\pi fT_d)}$$
最終的な式は次のようになる。
$$|H(f)| = 2|\sin(\pi fT_d)|$$
3. グラフ
Td = 1us の場合を例にCDSの周波数応答をグラフ化すると、以下のよう1000kHz周期のくし型の特性になる。
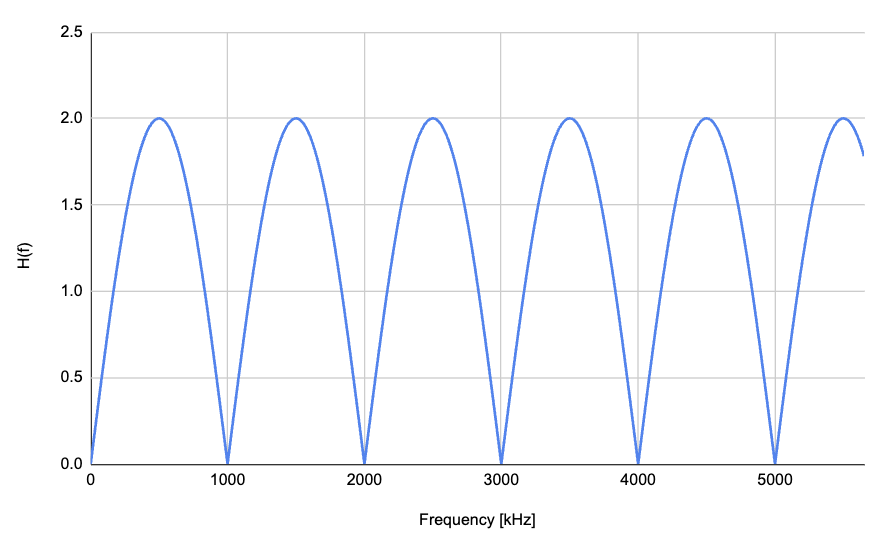
これは特定の周波数でゼロになる「くし型フィルター」の特性を示す。この特性により、CDSは特定の周波数成分を周期的に抑制し、ノイズ除去やオフセット補正に利用される。
コメント